Risk Metrics: beta 'β', correl 'ρxy', stdev 'σ', variance 'σ²'

Aug 28, 2020

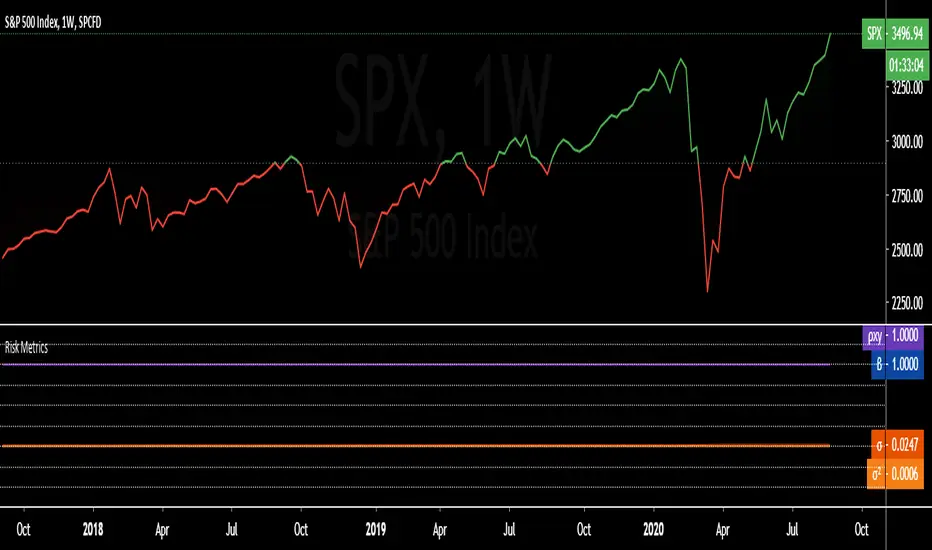
Portfolio Risk Metrics (Part I):

beta 'β'

The beta coefficient can be interpreted as follows:

β =1 exactly as volatile as the market
β >1 more volatile than the market
β <1>0 less volatile than the market
β =0 uncorrelated to the market
β <0 negatively correlated to the market

excerpt from the Corporate Finance Institute

correlation coefficient 'ρxy'

The correlation coefficient is a value that indicates the strength of the relationship between variables.
The coefficient can take any values from -1 to 1. The interpretations of the values are:

-1: Perfect negative correlation. The variables tend to move in opposite directions
(i.e., when one variable increases, the other variable decreases).

0: No correlation. The variables do not have a relationship with each other.

1: Perfect positive correlation. The variables tend to move in the same direction
(i.e., when one variable increases, the other variable also increases).

excerpt from the Corporate Finance Institute

standard deviation 'σ'

68% of returns will fall within 1 standard deviation of the arithmetic mean
95% of returns will fall within 2 standard deviations of the arithmetic mean
99% of returns will fall within 3 standard deviations of the arithmetic mean

excerpt from Corporate Finance Institute

variance 'σ²'

In investing, variance is used to compare the relative performance of each asset in a portfolio.
Because the results can be difficult to analyze, standard deviation is often used instead of variance.
In either case, the goal for the investor is to improve asset allocation.

excerpt from Investopedia

Aug 28, 2020

Release Notes

Conversion from percentages to decimals for better plot/visualization consistency.
Added ρxy² (correlation squared).